Математические модели вычислений
Альтернативные модели вычислений
Клеточные автоматы
Понятие «Тьюринг-полноты» в компьютерных языках
μ-рекурсивные функции Клини
Операторные схемы программ
Схемы Янова
maxim.krivchikov@gmail.com
https://maxxk.github.io/formal-models/
Клеточный автомат
Решётка («таблица» произвольной размерности) из ячеек, каждая из которых может находиться в конечном числе состояний.
На каждом шаге следующее состояние каждой ячейки определяется по заданному фиксированному правилу, которое может использовать текущее состояние ячейки и текущие состояния ячеек в некоторой окрестности.
Более строго:
- Пространство ячеек C.
- Конечный набор возможных состояний ячеек — Σ, |Σ| = k; ∀ c ∈ C, σ(c) ∈ Σ.
- Понятие окрестности ячейки — N(c) — конечное множество ячеек из C. Для всех ячеек окрестность имеет один и тот же размер |N(c)| = n. Окрестность «взаимна» — для каждой ячейки d из окрестности ячейки c, c ∈ N(d).
- Правило перехода φ : Σn → Σ.
На каждом шаге t правило перехода одновременно применяется к каждой ячейке с состояниями окрестности на предыдущий момент времени t-1.
Типы поведения автоматов
Классификация правил перехода Вольфрама:
Класс 1. Быстрая стабилизация состояния и его гомогенность.
Класс 2. Быстрая стабилизация состояния либо возникновение колебаний. Локальные изменения в начальных условиях оказывают локальный характер на дальнейший ход эволюции системы.
Класс 3. Почти все начальные условия приводят к псевдо-случайным последовательностям, стабильные структуры почти сразу уничтожаются окружающим шумом.
Класс 4. Результатом эволюции почти всех начальных состояний являются структуры, которые взаимодействуют сложным образом с формированием локальных, устойчивых структур, которые способны сохраняться длительное время.
Некоторые клеточные автоматы демонстрируют поведение, достаточное для эмуляции машины Тьюринга.
Литература: Клеточные автоматы: Stephen Wolfram. A New Kind of Science. Wolfram Media, Inc. 2007
Тьюринг-эквивалентные клеточные автоматы
- Игра «Жизнь» Конвэя (и ещё одна схема)
- «Rule 110» — одномерный клеточный автомат
Дополнительно:
- Эмулятор одномерного клеточного автомата (источник)
- Эмулятор двумерного клеточного автомата: http://golly.sourceforge.net/
- Эмулятор игры Тетрис в игре "Жизнь": https://codegolf.stackexchange.com/q/11880
- Универсальная машина Тьюринга в игре "Жизнь": http://rendell-attic.org/gol/utm/index.htm
Rule 110
Из Wolfram MathWorld: http://mathworld.wolfram.com/Rule110.html
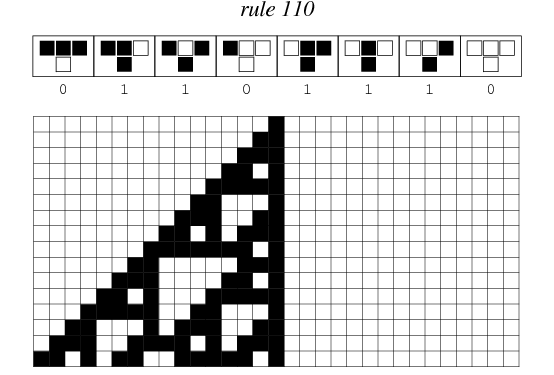
Эмуляция машины Тьюринга правилом 110
Машины Тьюринга можно эмулировать tag-системой Поста. Тэг-система Поста считывает по 2 (в общем случае — n) символов с начала ленты с данными, определяет на основе первого символа новую последовательность символов («дополнение») и дописывает её в конец ленты.
Тэг-систему можно эмулировать циклической тэг-системой: на ленте могут быть только символы Y, N; программа задаётся зацикленной последовательностью дополнений; если считан символ Y, текущее дополнение дописывается в конец и машина переходит к следующему дополнению, если N — машина просто переходит к следующему дополнению.
Циклическая тэг-система эмулируется системами глайдеров — движущихся (по прямой) точек разного типа (тип задаёт направление движения), при столкновении которых из точки могут начать движение глайдеры другого типа.
Система глайдеров эмулируется правилом 110.
Понятие «Тьюринг-полноты» в компьютерных языках
Машины с регистрами
Машина с регистрами включает:
- Неограниченное (как правило, конечное) количество именованных регистров, каждый из которых может содержать одно неотрицательное число неограниченного размера.
- Набор меток.
- Ограниченный набор инструкций, который может
включать:
- Арифметические инструкции (Increment(r), Decrement(r), Clear-to-zero(r), Load-constant(r, k), Add, Subtract, ...)
- Управляющие инструкции (Copy(r1, r2), LoadAccumulator(r), StoreAccumulator(r))
- Условный переход (обязательно; как правило, по заданному регистру): Jump-if-zero, Jump-if-not-zero, Jump-if-equal, ...
- Операции непрямой адресации (Load-from-address(r), Store-by-address(r))
- Ввод-вывод
- Регистр состояний — содержит текущую инструкцию и её адрес в программе.
- Список инструкций с метками (как правило, последовательный).
Классы: машины со счётчиками, машины с указателями, машины с памятью с произвольным доступом, машины с памятью с произвольным доступом с программой в регистрах (архитектура фон Неймана)
«Аппаратные» реализации
URISC (Ultimate Restricted Instruction Set Computer) — машина с одной инструкцией. Для того, чтобы иметь возможность эмулировать машину Тьюринга, память должна быть бесконечной, а адреса и ячейки — произвольными целыми числами (возможно, неотрицательными)
subleq a, b, c— посчитатьM[b] - M[a], записать вM[b]и, еслиb ≤ 0перейти на адресc. В памяти хранятся тройкиa, b, cdln a, b— уменьшить на 1 значениеM[a]; если получился0, перейти по адресуb
Механизм защиты памяти в x86-процессорах допускает реализацию
subleqс помощью вложенных исключений page faultMagic: The Gathering (и другие примеры на странице Accidentally Turing-complete)
μ-рекурсивные функции Клини
Частично-рекурсивные функции на натуральных числах.
Функции
- k-арные константные функции Kkn.
Kkn(x1, …, xk) = n
- 1-арная функция увеличения на 1
S(x) = x + 1
- Функции проекции Pki Pki(x1, …, xk) = xi
Операторы
- Оператор подстановки ∘ для m-арной функции h и m k-арных функций gi определяет k-арную функцию
h ∘ (g1, …, gm) = f(x1, …, xk)
f = h(g1(x1, …, xk), …, gm(x1, …, xk))
μ-рекурсивные функции Клини
Операторы
- Оператор примитивной рекурсии («цикл») ρ(g,h) по k-арной функции g (база индукции) и k+2-арной функции h (шаг индукции) определяет k-арную функцию f:
f(0, x1, …, xk) = g(x1, …, xk)
f(y+1, x1, …, xk) = h(y, f(y, x1, …, xk), x1, …, xk)
Первые два аргумента h — число итераций и результат предыдущей итерации.
- Оператор минимизации μ для k+1-арной полной функции f возвращает k-арную частичную функцию, которая находит минимальное значение первого аргумента z, при котором f(z, x1, …, xk) = 0:
μ(f)(x1, …, xk) = z : f(z, x1, …, xk) = 0; f(i < z, x1, …, xk) > 0
Компилятор подмножества😕 рекурсивных функций в машину Тьюринга
Операторная схема программы
Классический советский подход к теории программирования, предложенный А.А. Ляпуновым в первом курсе «Принципы программирования», который он читал в 1952/53 году на кафедре вычислительной математики.
В более позднем определении А.П. Ершова:
Задано конечное множество операторов F = { F1, …, Fn}. Входы и выходы описываются в терминах полюсов операторов P = A ∪ R — объединение непересекающихся множеств аргументов A = {a1, …, ap} и результатов R = { r1, …, rq }. Распределение полюсов — отображение V : P → F.
Граф переходов — ориентированный граф C = (F, J), где J — бинарное отношение, задающее для оператора его преемников по передаче управления. Компоненты связности графа переходов — отдельные программы в программном комплексе.
Скелет программы — набор перечисленных множеств S = (F, C, A, R, V).
Память описывается множеством X = { x1, …, xm } и распределяется среди полюсов отображением L : P → X.
Операторная схема программы — набор G = (S, X, L).
Задача экономии памяти
А.П. Ершов в книге (ссылка ниже) рассматривает задачу экономии памяти: каким образом можно использовать минимальное множество памяти X, сохраняя семантику программы?
Постановка задачи: по заданной схеме программы с распределением памяти L построить новое распределение памяти L', использующее, по возможности, память меньшего объёма.
А. П. Ершов. Введение в теоретическое программирование: беседы о методе. М.: Наука, 1977. 288 С.
Задача экономии памяти
Информационный граф I = (P, M) — двудольный граф M ⊂ R×A, который сопоставляет результаты оператора с аргументами его преемников. Маршрут информационной связи — путь в информационном графе, задаётся первым результатом и последним аргументом.
Компоненты связности информационного графа называются областями действия.
Области действия несовместимы тогда и только тогда, когда в каждой из них найдутся результаты r и r', соответственно, такие, что:
- V(r) = V(r') или
- V(r) — внутренний оператор маршрута информационной связи (r', a')
- V(r') — внутренний оператор маршрута информационной связи (r, a)
Задача экономии памяти решается выделением несовместимых областей действия раскраской графа и объединением совместимых областей действия.
Схема Янова
Модификация операторной схемы программ. Область приложения — исследование способов задания условий в программе и эквивалентных преобразований программ с условиями.
Не рассматривается понятие памяти и распределения памяти. Все операторы одноместны, принимают на вход исходное состояние памяти и возвращают полностью изменённое состояние.
Вводятся счётные множества предикатных символов P = { p1, p2, … } и операторных символов A = { A1, A2, … }.
Оператор A = A(P) — пара из операторного символа A и некоторого (возможно, пустого) множества предикатных символов P, которое называется сдвигом оператора A.
Схема Янова
Граф переходов — ориентированный граф, множество вершин которого состоит из неотрицательного числа преобразователей, распознавателей и одного останова. Из преобразователя выходит в точности одна дуга, из распознавателя — две различные (плюс-стрелка и минус-стрелка). Выделяется одна входная вершина графа и помечается входной стрелкой.
Преобразователи помечены операторными символами, распознаватели помечены логическими формулами над предикатными символами.
Схема Янова G(p1, …, pk)
Схема Янова

Семантика схемы Янова
Для того, чтобы схема задавала программу, необходимо дать интерпретацию операторным и предикатным символам, и описать алгоритм выполнения интерпретированной схемы.
Дано некоторое множество состояний памяти D. Предикатные символы pi соответствуют предикатам πi : D → { f, t }. Сами pi в программе назовём предикатными переменными.
Операторным символам Aj сопоставляются (возможно, частичные) функции φj : D → D
Выполнение схемы Янова
Начальный шаг. Берём произвольное d ∈ D в качестве исходного состояния памти и присваиваем значения всем предикатным переменным pi ≡ πi(d). Передаём управление на входную вершину графа переходов.
Шаг выполнения. Пусть d — текущее состояние памяти, Δ = (σ1, …, σk) — текущие значения предикатных переменных, S — текущая вершина графа переходов.
- Если S — останов, то выполнение завершается, и d является результатом выполнения схемы в данной интерпретации.
- Если S — распознаватель с условием F(p1, …, pk). Вычисляем σ = F(Δ) и передаём управление по плюс-стрелке, если σ=t и по минус-стрелке, если σ=f.
- Если S — преобразователь Aj(Pj), вычисляем новое состояние памяти d' = φj(d) и значения предикатных переменных в сдвиге Pj : pi ≡ πi(d'). Управление передаётся на следующую вершину графа.
Таким образом, получена частичная функция d = FG,I(d0).
Эквивалентность схем
Схемы G1 и G2 сравнимы, если они заданы над одним и тем же множеством предикатных символов, а также у одинаковых операторов совпадают сдвиги.
Две сравнимые схемы эквивалентны в некоторой совместной интерпретации I, если FG1,I(d) = FG2,I(d).
Две сравнимые схемы функционально эквивалентны, если они эквивалентны в любой совместной интерпретации.
Операционная история (след) интерпретированной схемы Янова HG,I(d) — полная последовательность выполняемых операторов и наборов значений функциональных переменных. Для исключения циклов вершины графа помечаются наборами значений предикатных переменных. Если при выполнении мы попали в вершину, помеченную таким же набором значений, что и текущий набор Δ, считаем, что мы попали в бесконечный цикл.
Две сравнимые схемы операционно эквивалентны, если они одинаково работают в любой совместной интерпретации, т.е. HG1,I(d) = HG2,I(d).
Теорема. Функциональная эквивалентность равносильна операционной эквивалентности.
Эквивалентность схем
Конфигурации схемы k ∈ K(G) строятся аналогично операционным историям, но без заданной интерпретации индуктивно:
Начальный шаг. Выберем произвольный набор исходных значений предикатных переменных Δ. Очередной шаг. Текущий набор Δ, текущая вершина S. Уже обработанные вершины помечены.
- Если S — помеченный распознаватель, то мы попали в пустой цикл и конфигурация не может быть построена.
- Если S — непомеченный распознаватель с условием F, помечаем его, вычисляем F(Δ) и переходим к вершине-преемнику.
- Если S — останов, построение конфигурации завершено.
- Если S — оператор, то записываем Ai в конфигурацию, и в качестве нового значения Δ' помещаем произвольный набор, образующий с набором Δ допустимую пару для оператора Ai.
Две сравнимые схемы формально эквивалентны, если их множества их конфигураций совпадают.
Теорема. Функциональная эквивалентность равносильна формальной эквивалентности.
Эквивалентные преобразования
Теорема. Для любых двух эквивалентных схем Янова можно построить последовательность эквивалентных преобразований, которые приводят их к общему виду.
Теорема. Задача эквивалентности двух сравнимых схем Янова разрешима.
Подловченко Р. И. К вопросу об эквивалентных преобразованиях алгоритмов и программ // Математические вопросы кибернетики. Вып. 9. — М.: Физматлит, 2000. — С. 25–36. URL: http://library.keldysh.ru/mvk.asp?id=2000-25
Задачи
- Задача 3.1*
- реализуйте интерпретатор μ-рекурсивных функций Клини с возможностью пошагового выполнения.
- Задача 3.2**
- реализуйте проверку числа на простоту в терминах μ-рекурсивных функций Клини.
- Задача 3.3*
- реализуйте интерпретатор произвольных клеточных автоматов с "квадратными" клетками, в качестве примера покажите работоспособную реализацию игры "жизнь".
- Задача 3.4***
- предложите возможные способы задания «системы типов», не допускающей задание незавершимых функций, для клеточных автоматов или для μ-рекурсивных функций Клини (с доказательством).
- Задача 3.5***
- опишите в терминах схем Янова один из алгоритмов сортировки списка и докажите его корректность.
- Задача 3.6**
- верно ли, что "классический" глайдер для двумерного клеточного автомата с «обычной» окрестностью работает только для правила Game of Life? Аналогичный вопрос про «линейку» из трёх заполненных клеток.