Формальные модели программ
\(λ\)-исчисление как формальная система. Парадокс Клини-Россера: Тьюринг-полные системы противоречивы
Теория типов: первый шаг (от Principia Mathematica) до \(λ\)-исчисления с простыми типами
Соответствие Карри-Говарда: программа = доказательство утверждения (интуиционистская логика)
Основные свойства типизированного \(λ\)-исчисления
Материалы курса: https://maxxk.github.io/formal-models-2015/
По следам наших публикаций
Из большого результата иногда можно выделить не менее важный меньший результат
Конечный автомат — более простая модель, чем машина Тьюринга, был описан в 1943 году — через 7 лет после публикации Тьюринга (и без связи с ним)!
Направление дальнейшего изучения
Model checking позволяет доказывать низкоуровневые свойства. Наша задача — научиться доказывать свойства высокоуровневые; двигаться между уровнями абстракции, сохраняя справедливость доказательств.
В этом нам поможет современная интуиционистская теория типов, к которой мы будем подходить со стороны типизированного \(λ\)-исчисления.
Нетипизированное \(λ\)-исчисление Чёрча (1932)
Рассмотрим формулы, составленные из выражений вида:
- \(λ x . F\) — абстракция (\(x\) — имя переменной, которая может встречаться в формуле \(F\))
- \(x, y, z, …\) — переменная
- \(A · B\) — приложение (аппликация), \(A, B\) — формулы.
Введём правило переписывания (\(β\)-редукция):
\[ (λx. F) · G ⟶_β F[G/x] \]
Буква \(α\) зарезервирована для понятия \(α\)-эквивалентности — формулы, эквивалентные с точностью до переименования переменных.
Вычисление считается завершённым когда нет \(β\)-редексов (подформул, к которым применима \(β\)-редукция)
Оригинальная формулировка Чёрча

Church A. A Set of Postulates for the Foundation of Logic // The Annals of Mathematics. 1932. Vol. 33, № 2. P. 346–366.
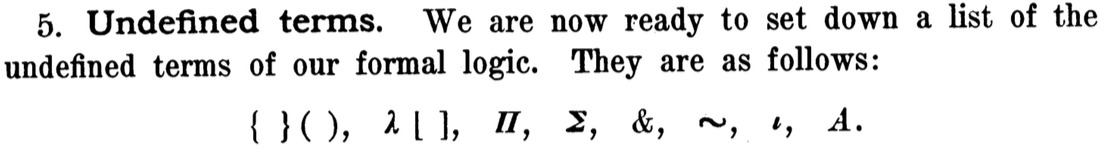
Оригинальная формулировка Чёрча
- { } ( )
- аппликация (чтобы проще выделять левую и правую части)
- λ []
- абстракция
- Π(F, G)
- G(x) выполняется для всех значений, для которых выполняетсы F(x)
- Σ(F)
- существует значение x, для которого верно F(x)
- &
- конъюнкция
- ~
- отрицание (¬)
- ɩ (F)
- такое x, что F(x) верно
- A(F, M)
- «абстракция M относительно F», дизъюнкция, используется для определения классов в стиле Principia Mathematica
Комбинаторная логика
M. Schönfinkel (1924), H. Curry (1930)
Формальная система, синтаксис которой состоит из переменных, парных скобок и комбинаторов (правил преобразования строк символов). Эквивалентна машине Тьюринга, близко связана с \(λ\)-исчислением.
- S x y z = x z (y z) — распределение
- K x y = x — отмена
- (S, K — базис, из них можно получить остальные комбинаторы)
- I x = x — идентичность
- C x y z = x z y — перестановка
- B x y z = x (y z) — композиция
- W x y = x y y — копирование
- Y x = x (Y x) — неподвижная точка
Y-комбинатор — примитивный комбинатор рекурсии. Если вместо переменных использовать \(λ\)-абстракцию и арифметические выражения, наивная реализация факториала могла бы выглядеть так:
Fact := Y (λ fact. λ x.
if (x == 0) return 1
else return x*fact(x - 1))Парадокс Карри
1935 (Клини, Россер), 1941 (Карри), 1942 (Карри)
Если дана формальная система, удовлетворяющая следующим свойствам:
- конечное число примитивных термов, единственная операция — бинарная операция приложения, единственный унарный предикат — предикат выводимости «⊦ A»
- определено равенство в терминах примитивного терма Q и приложения (X = Y ≡ ⊦ Q X Y)
- равенство симметрично, транзитивно, сохраняется при аппликации и подразумевает взаимную выводимость (A = B ∧ ⊦ A ⟹ ⊦ B)
- для любого терма \(M\) со свободными переменными \(X_1, …, X_n\) существует терм $M^* $, такой, что \(M^* · X_1 · … · X_n = M\)
может быть определён оператор импликации \(⊃\), такой, что для любых термов \(M, N\):
- ⊦ M ⊃ M
- ⊦ M ⊃ (M ⊃ N) ⟹ ⊦ M ⊃ N
- ⊦ M и ⊦ M ⊃ N ⟹ ⊦ N
Парадокс Карри
...то любой терм B выводим с помощью следующего построения:
- Для любого A, если A = A ⊃ B ⟹ ⊦ B (лемма)
- N ≡ λ X . X ⊃ B
- R ≡ λ Y . N (Y · Y)
- A ≡ R R (= N(R R) = N A = A ⊃ B и B выводимо)
П.1 — «плохой» терм.
Основная идея — если формальная система допускает неограниченный оператор рекурсии, то она противоречива. Это справедливо для любой формальной системы, эквивалентной комбинаторной логике или λ-исчислению.
Principia Mathematica
B. Russel, A. Whitehead. 1910 – 1913 (3 тома).
— фундаментальный труд по формализованным основаниям математики.
В книгах используется слегка отличающаяся от современной логическая нотация, но в целом их достаточно легко понять.
Авторы (до результатов Гёделя) пытались описать математику с позиций формализма и в этом преуспели.
Для того, чтобы преодолеть парадокс Рассела, предлагалось рассматривать объекты как принадлежащие к некоторым типам. Типы определяются как область истинности некоторого утверждения.
При изучении функций комплексного переменного, мы не пытаемся подставить вместо аргумента, например, бесконечномерный оператор. Все утверждения формируются с подразумеваемым условием «x — комплексное число».
Типы позволяют избавиться от циклических определений.
λ-исчисление с простыми типами
1940 (Чёрч); далее представлено определение, ближе к современной записи.
http://plato.stanford.edu/entries/type-theory-church/
Пусть дано множество базовых типов B, * ∈ B
Допустимые типы:
\[ τ ≡ b \; | \; τ_1 → τ_2, \qquad b ∈ B. \]
Стрелка — правоассоциативна:
α → β → γ ≡ α → (β → γ)
Сокращение: α' ≡ α → α
* — «тип типов», тип высказываний
У Чёрча — в обратном порядке и без стрелок (α → β → γ ≡ (γβα))
Формулы:
- Символы λ, [, ] для описания абстракции
- Переменные \(a_α\), \(b_α\), … типа α
- Логические константы :
- \(¬_{* → * }\) отрицание
- \(∨_{* → * → * }\) дизъюнкция,
- \(Π_{(α → * ) → * }\) универсальная квантификация,
- \(i_{(α → * ) → α}\) оператор выбора
- \(¬_{* → * }\) отрицание
- Константы произвольных типов α
Современная формулировка исчисления (только вычислительная часть) не содержит логических констант и типа * (точнее, * — это «тип всех типов», но не входит в константу τ)
λ-исчисление с простыми типами
Грамматика:
- Абстракция (записывается как $λ x_α [ A_α ] $)
- Приложение
- Константы и переменные
У Чёрча индексы типов обязательны, но мы будем их пропускать, если это уместно и использовать отношение типизации.
Отношение типизации
Окружение типизации Γ — конечный набор высказываний \(x : α\) (x имеет тип α), где \(x\) — символ переменной, а \(α\) — тип.
[] — пустое окружение, \(x : α ∈ Γ\) записывается как суждение \(Γ ⊦ x : α\) (из окружения выводимо, что x имеет тип α).
\(Γ, x : α\) — окружение Γ, расширенное суждением \(x : α\).
Расширенная грамматика и правила вывода исчисления задаются в терминах таких суждений — правил типизации (и известного нам правила β-редукции)
$ \dfrac{c_α \text{— константа типа α}}{Γ ⊦ c : α}$, включая логические константы, если мы их рассматриваем
$ \dfrac{Γ, x : σ ⊦ e : τ}{λx_σ.e : σ → τ}$, обычно абстракция записывается как $λ x : σ . e $
$ \dfrac{Γ ⊦ x : σ → τ, \qquad Γ ⊦ y : σ}{Γ ⊦ x_{σ → τ} · y_σ : τ}$
Допустимы только типизируемые формулы, т.е. те, для которых из данного окружения можно вывести тип.
Аксиомы и правила вывода
- $ (λ x . F) · G ⟶_β F[G/x]$
- β-редукция
Если используются логические константы, то импликация, как в алгебре логики \(A_o ⊃ B_o ≡ (¬A)∨B\) и Modus Ponens (A ⊃ B, A ⟹ B)
- \([p_* ∨ p_*] ⊃ p_*\)
- \(p_* ⊃ [p_* ∨ q_*]\)
- \([p_* ∨ q_*] ⊃ [q_* ∨ p_*]\)
- \([p_* ⊃ q_*] ⊃ [[r_* ∨ p_*] ⊃ [r_* ∨ q_*] ]\)
(5\({}^α\)) \(Π_{(α → *) → *} f_{α → *} ⊃ f_{α→*} x_α\)
(6\({}^α\)) \(∀x_α[p_* ∨ f_{α → *} x_α] ⊃ [p_* ∨ Π f_{α→*}]\)
(и еще несколько аксиом в оригинале)
Естественная дедукция
τ ≡ b | α → β
Правила типизации, используемые для определения типов, можно структурировать (следующая структура носит название «естественная дедукция», natural deduction):
- формация (Formation) — как определяется конструктор типа
- $ \dfrac{α, β\text{ — типы}}{α → β \text{ — тип}} $
- введение (Introduction) — как определяются элементы типа
- $ \dfrac{Γ, x : σ ⊦ e : τ}{λx_σ.e : σ → τ}$
- удаление (Elimination) — что можно делать с элементами типа
- $ \dfrac{Γ ⊦ x : σ → τ, \qquad Γ ⊦ y : σ}{Γ ⊦ x_{σ → τ} · y_σ : τ}$, \(x\) — удаляемый терм
- редукция (Reduction) — взаимное уничтожение термов введения и удаления (не входит в обычное понятие естественной дедукции)
- \(\underbrace{\overbrace{\large (λ x . F)}^{\small введение} {\large ·} {\large G}}_{\small удаление} ⟶_{β} F[G/x]\)
Свойства типизированного λ-исчисления
- сохранение типизации правилами редукции (\(x : α ⟶ y : α\))
- теорема Чёрча-Россера: β-редукция конфлюэнтна
правила редукции можно применять в разном порядке (λ x . \overbrace{f · (\underbrace{g · x})})
если \(x ⟶ y\) и \(x ⟶ z\) с помощью разной последовательности применения правил редукции, то существует терм \(w\), для которого \(y ⟶ w\) и \(z ⟶ w\)
«свойство ромба»
Нормализация
Редекс — терм удаления, для которого есть правило редукции.
Нормальная форма терма относительно редукции — это такой вид, при котором к нему неприменимы правила редукции.
Головная нормальная форма терма — если в головной позиции (корне дерева) не стоит редекс.
Нормализация — свойство формальной системы: если у терма есть нормальная форма, то она единственная.
Сильная нормализация — у всех термов есть единственная нормальная форма (= нет термов, редукция которых не завершается).
Сильная нормализация для просто типизированного λ-исчисления
Просто типизированное λ-исчисление обладает свойством сильной типизации.
Доказательство такого свойства выполняется с помощью моделей —
Эквивалентность термов
Обычно определяется следующим образом: A эквивалентен B, если A и B приводятся β-редукцией к идентичному виду, с точностью до корректных (не меняющих) переименований переменных. На индексах де Брёйна последнее замечание неактуально.
η-эквивалентность
Пусть \(f : α → β\). Тогда \(λ (x : α). f · x\) интуитивно эквивалентен исходной \(f\), но по указанному выше определению формально это разные термы.
η-эквивалентность включает такое понятие и, в случае просто типизированного λ-исчисления, не нарушает разрешимости эквивалентности типов.
Проверка типов разрешима — если есть алгоритм, который для любого терма определяет, корректно ли он типизирован.
Эквивалентность термов разрешима — если есть алгоритм, который для любой пары термов определяет, эквивалентны ли они при заданных правилах.
Соответствие Карри-Говарда для просто типизированного \(λ\)-исчисления
Типы — импликативные суждения. Доказательства — термы, имеющие этот вид.
Если ввести тип ложных высказываний как базовый тип False без правил введения и с правилом удаления ex falso, можно ввести и отрицание — «не α» ≡ α → False.
Двусторонняя проверка типов
Алгоритм проверки типов.
Достаточны аннотации типов у констант и переменных абстракции, остальные — можно вывести.
Две взаимно-рекурсивные функции — check и infer.
infer выводит тип терма, check проверяет, что терм имеет заданный тип.
Опциональные аннотации.
Не все утверждения удобно представимы в λ-исчислении с простыми типами
В частности, для нумералов Чёрча представимый класс называется «расширенные полиномы» над ℕ:
- 0, 1, проекции
- сложение, умножение
- функция
ifzero(n, m, p) =ifn = 0thenmelsep
В следующий раз мы рассмотрим различные способы расширения набора типов и постараемся убрать разделение между типами и термами.
Задачи со звёздочкой
Задача 5.1** Реализовать алгоритм двусторонней проверки типов для λ-исчисления с простыми типами (синтаксис входных данных — на ваше усмотрение).
- бонусная * — добавить редукцию
- бонусная * — визуализация редукции
Задача 5.2* Реализовать нумералы Чёрча с операцией сложения.
- бонусная * — умножение
- бонусная * — нетривиальный пример расширенного полинома