Software and Programming Language Theory

Denotational semantics implementation

Monads

Monad Transformers

Effects

Domains and Fixed point semantics

Course page: https://maxxk.github.io/programming-languages/ Contact author: maxim.krivchikov@gmail.com

Previous class: Imp’

Simple imperative language with arithmetical and boolean expressions, assignment, conditional operator and loop.

Abstract syntax (omitting the operator precedence and lexical structure):

Program = Statement "return" VariableName

Statement = VariableName "=" ArithmeticalExpression
| "skip"
| Statement (";" | "\n") Statement
| "if" "(" BooleanExpression ")" "{ " Statement " } else { " Statement " }"
| "while "(" BooleanExpression ")" "{ " Statement  "}"

ArithmeticalExpression = VariableName
| IntegerNumber
| "sqrt" ArithmeticalExpression
| "-" ArithmeticalExpression
| ArithmeticalExpression ("+" | "-" | "*" | "/" | "%") ArithmeticalExpression

BooleanExpression = ArithmeticalExpression ("<" | ">" | "==") ArithmeticalExpression
| "!" BooleanExpression
| BooleanExpression ("&&" | "||" | "^^")

Previous class: Imp’ programs

1. a, b, c are the quadratic equation coefficients.

d = sqrt(b*b - 4*a*c)
x1 = (-b + d) / 2*a
x2 = (-b - d) / 2*a
if (x1 > x2) {
  res = x1
} else {
  res = x2
}
return res

2. Primality test for n. Returns 0 if n is prime, otherwise returns minimal n divisor.

bound = sqrt(n)
i = 2
divisor=0
while (i < bound && divisor == 0) {
  if (n % i == 0) { divisor = n } else { skip };
}
return divisor

Denotational semantics implementation

Evolution of statement meaning function for Imp’ (from previous class):

1. Trivial case

⟦ · ⟧_S : VariableState → VariableState

⟦skip⟧ = λenv.env

2. Exceptions possible during expression evaluation.

New notation: domain of answers A = VariableState + Error

⟦ · ⟧_S : VariableState → A

⟦skip⟧ = λenv.inl(env)

3. Continuations for complex control flow, conceptually.

⟦ · ⟧_S : VariableState → (c_break : VariableState → A)→

   → (c_continue : VariableState → A) → A

⟦skip⟧ = λenv.c_break.c_continue.inl(env)

Denotational semantics implementation

Finally, for a real language we end up with four meaning functions for statements.

(Source: N. Papaspyrou. A Formal Semantics for the C Programming Language).

Note that almost a half of the domains employed are not simply-constructed, they are defined as the application of an argument to a domain-generating function.

We need an approach to split the semantics to some modular functions.

Imp’ expression semantics

Under normal circumstances we do not care about exceptions if they are passed through the normal computation flow, we even defined withLeft function for it:

withLeft : (f : X → Y) → X + Error → Y + Error
withLeft(f, x) = match(x)  
▷ inl a ↦ f(a)
▷ inr e ↦ e
end

• left composition: x >>= y ≡ withLeft(y, x)
• left variable binding: a ← b; S ≡ withLeft(λa. S, b)

⟦ − e⟧ = λenv.x ← ⟦e⟧(env);  − x

⟦Identifier(I)⟧ = λenv.inl(env(I))

…

Now let us mark the following three parts of our notation:

1. The type constructor wraps a value in some way:

·  + Error : Type → Type

2. inl injection operator lets us wrap an actual computation result to fit an application result of the type constructor:

inl : A → A + Error

3. withLeft’ binding function allows us to transform the wrapped value by function defined only on the unwrapped values:

withLeft’ : (f : X → Y + Error) → X + Error → Y + Error

Standard monads

We can equip simpe type constructors with two functions which satisfy the monad laws and get standard monads. Examples from Haskell mtl library.

Exception monad

Exception E A = A + E 
return x = inl x 
bind f x= match(x)  
▷ *inl* a ↦ f(a) 
▷ *inr* e ↦ e 
end 

throw : Error → A + Error
catch : A + Error → (Error → A + Error) → A + Error

Standard monads

Reader monad

The read-only environment

Reader R A = R → A
return x = λ env. x
bind f x = λ env. f(x(env))

ask : Reader R A (get local state)
local : (R → R) → Reader R A → Reader R A (locally modify environment)
reader : (R → A) → Reader R A (get an environmet)

Standard monads

Writer monad

Models write-only output (logging, tracing).

0 : W
⊕ : W → W → W
⊕ is associative

Writer W A = A × W
return x = (x, 0)
bind f x = let (y, w) = f(fst x) in (y, snd x + w)

tell : W → Writer W True
listen : Writer W A → Writer W (A × W)
pass : Writer W (A × (W → W)) → Writer W A

Standard monads

State monad

Models the mutable state.

State S A = S → A × S
return x = λ s. (x, s)
bind f x = λ s. let (x', s') = x in (f(x'), s')

get : State S S 
put : S → State S ()
modify : (S → S) → State S ()
gets : (S → A) → State S A

Standard monads

List monad

Models the nondeterminism.

List A 
return x = [x]
bind f x = map f x

(helpers — all the standard functions of the list type)

Standard monads

Continuation monad

Models a complex control flow.

Cont R A = (A → R) → R
return x = λ k . k(x)
bind f x = λ k . x(λ m. f(m)(k))

x : (A → R) → R
f : A → (B → R) → R
bind f x : Cont R B = (B → R) → R

See also: https://gist.github.com/edsko/6bf6e8c93a2d1e7941b9

Monad transformers

Monad transformer is the following construction:

A transformer for type constructor:

t : (Type → Type) → Type → Type

A way to obtain monad implementations for transformed monads:

∀ m, Monad m → Monad (t m)

Lifting operator:

lift : ∀ (a : Type), m a → (t m) a
lift . return = return
lift (m >>= k) = (lift m) >>= (lift ∘ k)

The purpose of the monad transformer is to obtain a single object representing a stack of monads.

Extensible Effects

http://okmij.org/ftp/Haskell/extensible/index.html

http://docs.idris-lang.org/en/latest/effects/

Domains and Fixed Points

Loop semantics

⟦ while b s ⟧ = λ env. b' ← ⟦b⟧(env) ; 
  if b' = false
    env
  else ⟦ s ⟧(env) >>= ???

How can we define the meaning of the while loop? We can’t just remove the structural recursion requirement: we may define terms with bad behavior in untyped lambda-calculus.

Fixed point semantics

Usually complex recursive functions may be defined by the means of the fixed point combinator and the generating function.

Example: factorial:

n! = 1 if n=0
n! = n · (n-1)! otherwise

Generating function accepts the recursive call as another argument:

genFact = λ fact . λ n .
  if n = 0
    return 1
  else 
    return n · fact(n)

Suppose we call genFact first with identity function and then — by applying the genFact to result:

f₁ = genFact(λn.n), f₂ = genFact(f₁), …, f_k = genFact(f_k − 1), …

For some good-behaving generating functions (or for some good starting arguments) such a sequence will have fixed points:

f_∞ is a fixed point of genFact iff genFact(f_∞) = f_∞.

Fixed points

For the function [0, 1] → [0, 1]: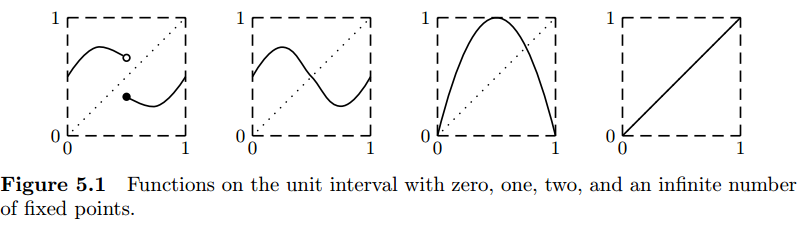

To define a proper recursive function we need to find a solution to the recursive equation: gen(f_∞) = f_∞. Under what conditions does this equation have a solution and how can we construct it?

Least fixed point

We need something like the following theorem, but for our lambda-definable function space:

Banach Fixed Point Theorem. Let (X, d) be a non-empty complete metric space with a contraction mapping T : X → X. Then T admits a unique fixed-point x* in X (i.e. T(x*) = x*).

Furthermore, x* can be found as follows: start with an arbitrary element x₀ in X and define a sequence {x_n} by x_n = T(x_n − 1), then x_n → x*.

The main contribution of D. Scott and Yu. L. Ershov which allows us to call them the creators of the denotational semantics is the construction which allows fixed points for some (continuous) functions.

Partial order

Partial order is a pair (D, ⩽) of a domain D and binary ordering relation ⩽ that is:

• reflexive (a ⩽ a)
• transitive (a ⩽ b, b ⩽ c ⇒ a ⩽ c)
• antisymmetric (a ⩽ b, b ⩽ a ⇒ a = b)

Pair of elements in D which are not in the ordering relation are called incomparable. Trivial example: discrete order in which all elements are incomparable. For Bool domain we usually define a discrete partial order. Partial order is total order if there is no incomparable elements.

Upper bound of subset X ⊆ D is an element u ∈ D that is “greater” (stronger) than any element in X:

∀ x ∈ X, x ⩽ u.

Some subsets may have even the least upper bound (upper bound which is “less” (weaker) than any other upper bound).

(and antisymmetrical lower bound and greatest lower bound)

Partial order lifting

Bottom element (⊥) is such an element which is weaker than any element in D, top element (⊤) is such an element which is stronger than any element in D.

Natural numbers ℕ with usual ordering have bottom element (0 or 1) but no top element. Discrete partial orders have neither.

Any partial order D may be lifted to another partial order D_⊥ that has all elements and orderings of D, but introduces new bottom element ⊥. Lifted discrete partial order is called flat partial order.

Partial order over constructors

We can define the partial order over simple (non-dependent) type constructors:

Product: (d, e) ∈ D × E; (d, e) ⩽ (d’, e’) iff d ⩽ d’ and e ⩽ e’

Sum: A+B;    inl a ⩽ inl a’ iff a ⩽ a’;    inr b ⩽ inr b’ iff b ⩽ b’.

Function: f, g ∈ D → E;    f ⩽ g iff ∀ d ∈ D, f(d) ⩽ g(d).

Sequence: D^*

• prefix ordering
• sum-of-products ordering

Powerdomain: 2^D, sets of all subsets under the subset ordering.

Complete partial orders (CPOs)

Chain is totally ordered nonempty subset of partial orer.

Partial order D is complete (CPO) iff every chain in D has least upper bound (limit).

Example: partial order Bool^* is not CPO under the prefix ordering, because the chain {[], [true], [true, true], …} has the infinite sequence of true as a limit, which is not a finite sequence.

We can extend it with Bool^∞ (set of all infinite boolean sequences), so that Bool^* ∪ Bool^∞ = Bool^* is a CPO

Theorem. For any CPOs D, E we can define the following CPOs under the defined orderings: D_⟂, D × E, D + E, D → E, D^* (under the sum-of-products ordering), D (under the prefix ordering).

Pointedness

A partial order is pointed if it has a bottom element.

Theorem. For any partial orders D, E:

• D_⟂ is pointed,
• D × E is pointed iff both D and E are pointed
• D + E is never pointed
• D → E is pointed iff E is pointed
• D^* under the sum-of-products ordering is never pointed
• D^* and D^* ∪ D^∞ under the prefix ordering are always pointed.

Monotonicity and continuity

f : D → E is monotonic (D, E are CPOs) iff x ⩽ y ⇒ f(x) ⩽ f(y).

f : D → E is continuous iff for any chain C ⊆ D, f(lub(C)) = lub({f(c) | c ∈ C})

In some sense least upper bounds and chains over CPOs are related in the same way as limits and filter bases in calculus.

Theorem. On finite CPOs (+ infinite CPOs with only finite chains) monotonicity implies continuity. On any CPO continuity implies monotonicity.

Least Fixed Point Theorem

Theorem. If D is a pointed CPO, then a continuous function f : D → D has a least fixed point fix(f) defined by lub{fⁿ(⟂), n ⩾ 0}.

So, if we can prove our function is continuous, we can use fixed point combinators.

Example:

genFact : (fact : ℕ → ℕ) → ℕ → ℕ

genFact = λ fact . λ n .
  if n = 0
    return 1
  else 
    return n · fact(n)

Use discrete order on ℕ and lift function to ℕ_⊥. Function space ℕ_⊥ → ℕ_⊥ is a CPO with order:

f ⩽ g ⇔ ∀ x : f(x) ⩽ g(x).

genFact is monotonic and continuous in ℕ_⊥ → ℕ_⊥, so we may use least fixed point operator.

Monads bibliography

1. Moggi E. Notions of computation and monads // Information and Computation. 1991. Vol. 93, № 1. P. 55–92.
2. Harrison W. Cheap (but functional) threads // Online
3. Danielsson N.A. Operational Semantics Using the Partiality Monad // Proceedings of the 17th ACM SIGPLAN International Conference on Functional Programming. New York, NY, USA: ACM, 2012. P. 127–138.
4. Papaspyrou N.S. A Resumption Monad Transformer and its Applications in the Semantics of Concurrency: CSD-SW-TR-2-01. Athenes, Greece: National Technical University of Athens, School of Electrical and Computer Engineering, Software Engineering Laboratory, 2001.

Some of previously discussed papers also use the monads, for example: 5. Danielsson N.A. Total parser combinators // Proceedings of the 15th ACM SIGPLAN international conference on Functional programming - ICFP ’10. ACM Press, 2010. P. 285–285.

Monad transformers: 6. Liang S., Hudak P., Jones M. Monad Transformers and Modular Interpreters // Conference Record of POPL’95: 22nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, San Francisco, CA, January 1995.

Extensible effects: 7. Papers on the page linked from previous presentation 8. Idris tutorial on the programming with effects

Homework assignments

Task 9.1 ** Extend the Imp’ denotational semantics with break and continue loop control statements (use continuation monad).

Task 9.2 ** Define the big-step operational semantics for Imp’ and make a short qualitative (textual) comparison between two definitions.

Task 9.3 ** Define a continuous meaning function for while loops in Imp’.

Task 9.4 *** For all “Standard monads” in this presentation prove that operators and helper functions are continuous.

Task 9.5 * Exercise 5.10 in Turbak, Gifford.