Software and Programming Language Theory
Dynamic semantics
Operational sematics
Programming language specification
Dynamic semantics
— the semantics of the programming language statements at the run time.
Approaches
Operational Semantics
The meaning of the program is specified as a sequence of computational steps for some abstract machine.
Axiomatic Semantics
The meaning of the program is defined in terms of effects on the program statements on assertions about the program state.
Denotational Semantics
The meaning of the program is formalized as a mathematical object (denotation).
Operational semantics
Program execution may be understood as a step-by-step process that evolves by mechanical application of a fixed set of rules.
Rules describe how language constructs affect the state of some abstract machine that provides the mathematical model of computation. Each state of the abstract machine is called configuration.
Operational execution model
Big-step and small-step operational semantics
Small-step operational semantics (Structural Operational Semantics, SOS): step-by-step transformation of configurations in abstract machine is defined by set of rewrite rules.
Big-step operational semantics (natural semantics): program execution is described in terms of recursive evaluation of subphrases of a program. Each nontrivial syntactic domain (subset of abstract syntax tree constructors) has its specific evaluation relation.
Structural operational semantics
Set-theoretic abstract machine model
Consider programming language L with well-formed, well-typed programs P ∈ Prog, inputs I ∈ Inputs and answers A ∈ AnsExp.
Structural operational semantics for L is five-tuple S = 〈 CF, ⇒, FC, IF, OF 〉
- cf ∈ CF — domain of configurations for an abstract machine
- ⇒ — transition relation, “⇒” ⊆ CF × CF. Two configurations are in transition relation iff there is a (one step) transition from cf to cf’
cf ⇒ cf’ ⇔ 〈 cf, cf’ 〉 ∈ ⇒
⇒* — reflexive transitive closure of ⇒. Sequence of transitions cf ⇒* cf’ is called transition path.
Configuration cf is reducible if there is some cf’ such that cf ⇒ cf’, otherwise cf is irreducible.
Transition relation ⇒ is deterministic if for every cf there is exactly one cf’, otherwise ⇒ is nondeterministic.
Structural operational semantics
Structural operational semantics for language L is five-tuple S = 〈 CF, ⇒, FC, IF, OF 〉
Irreducible — all irreducible configurations
FC — set of final configurations which yield the correct answer, FC ⊂ Irreducible
Stuck = Irreducible / FC — set of stuck states, nonfinal irreducible configurations (e.g. error states)
IF : (Prog × Inputs) → CF — input function, transforms a program and its inputs to an initial configuration
OF : FC → AnsExp — output function, maps a program and its inputs to an initial configuration
Program behavior
Outcome = AnsExp + ErrorResult (+ — disjoint union)
Deterministic behavior, if ⇒ is deterministic:
behdet : (Prog × Inputs) → Outcome
behdet 〈 P, I 〉 | IF 〈 P, I 〉 ⇒* cf ∈ FC = AnsExp ↦ Outcome (OF cf)
behdet 〈 P, I 〉 | IF 〈 P, I 〉 ⇒* cf ∈ Stuck = ErrorResult
behdet 〈 P, I 〉 | IF 〈 P, I 〉 ⇒∞ = ∞
Non-deterministic behavior
𝒫 (A) — powerset of A (set of all subsets of A).
beh : (Prog × Inputs) → 𝒫 (Outcome)
o ∈ beh( 〈P, I〉 ) if o = AnsExp ↦ Outcome (OF cf) and IF 〈P, I〉 ⇒* cf ∈ FC
o ∈ beh( 〈P, I〉 ) if o ∈ ErrorResult and IF 〈 P, I 〉 ⇒* cf ∈ Stuck
o ∈ beh( 〈P, I〉 ) if o = ∞ and IF 〈P, I〉 ⇒∞
Rewrite rules
Usually relations on complex domains are specified in terms of formal inference system.
| antecendents |
|---|
| consequents |
antecedents = ⊘ ⇒ rule is called axiom, otherwise progress rule.
Example axioms for stack-based language (placing constant on stack; configuration state = 〈 command sequence, stack 〉):
〈 N . Q, S〉 ⇒ 〈 Q, N . S 〉 [num]
〈 (Q) . R, S〉 ⇒ 〈 R, (Q) . S 〉 [seq]
| S = S1 . S2 . Sn |
|---|
| 〈 swap . Q, S〉 ⇒ 〈 Q, S2 . S1 . Sn 〉 |
If cf is a configuration in which first command in sequence is constant, then there is a transition from cf to cf’ in which constant is moved from command sequence to the top of the stack.
Example structural operational semantics execution

Subexpression evaluation

Evaluation contexts
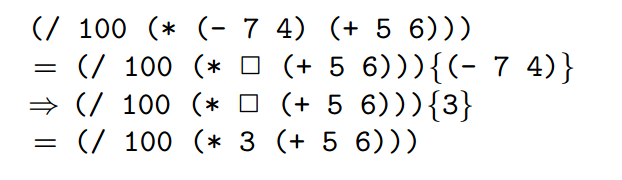
Big-step operational semantics
Big-step operational semantics (natural semantics): program execution is described in terms of recursive evaluation of subphrases of a program. Each nontrivial syntactic domain (subset of abstract syntax tree constructors) has its specific evaluation relation.
E.g. →NE for numerical expressions and →Prog for programs.
Big-step operational semantics

Language properties
Usually operational semantics is used to prove some of the following properties:
- universality: the language can express all computable programs;
- determinism: the set of possible outcomes from executing a program on any particular inputs is a singleton;
- strong normalization: all programs are guaranteed to terminate on all inputs (i.e., it is not possible to express an infinite loop);
- static checkability: a class of program errors can be found by static analysis without resorting to execution;
- referential transparency: different occurrences of an expression within the same context always have the same meaning.
Example proof of termination
Turbak, Gifford. p. 85
K Framework
Homework Assignments
Turbak, Gifford. Exercises 3.3, 3.4, 3.5, 3.6, 3.10a, 3.10b, 3.18, 3.19, 3.22, 3.24, 3.25 (one star each, at most 3 stars)