Software and Programming Language Theory

Typing

https://maxxk.github.io/programming-languages/

Literature

  • R. Harper, Practical Foundations for Programming Languages, 2nd ed, 2016.
  • B. Pierce. Types and Programming Languages. 2002.

Type system

A type system is a tractable syntactic method for proving the absence of certain program behaviors by classifying phrases according to the kinds of values they compute.

B. Pierce. Types and Programming Languages. 2002.

We can say that type system is a (usually) decidable approximation of programming language dynamic semantics.

Typing

The role of type system is to impose constraints on the formation of phrases that are sensitive to the context in which they occur.

In practice, typing is usually specified by means of the formal inference system:

  • typing judgement “in context Γ the expression x has type τ” — Γ ⊦ x : τ
  • context Γ — set of typing judgement for already defined variables or expressions
  • Γ, x : a ⊦ y : b

Simply Typed Lambda Calculus

Type: τ ≡ b | τ₁ → τ₂,

b is an element of the set of basic types.

Typing rules:

   
Γ, x : α ⊦ x : α
cα — constant of type α
Γ ⊦ c: α
Γ, x : σ ⊦ e : τ
Γ ⊦ (λ xσ . e) : σ → τ
Γ ⊦ x : σ → τ     Γ ⊦ y : σ
Γ ⊦ x · y : τ

Derivation — tree of rule applications which starts from empty context and ends in typing derivation for required expression.

Example from Harper’s «Practical Foundations…»

Type: τ ≡ num | str

Expression: e ≡ x (variable) | n |
s (number and string literals)
|
e + f (addition)
|
e ^ f (concatenation)
|
|e| (length)
|
let x be e in f (definition)

Typing:

   
Γ, x : α ⊦ x : α
   
Γ ⊦ s : str
   
Γ ⊦ n : num
Γ ⊦ e : num     Γ ⊦ f : num
Γ ⊦ e + f : num
Γ ⊦ e : str     Γ ⊦ f : str
Γ ⊦ e ^ f : str
Γ ⊦ e : str
Γ ⊦ |e| : num
Γ ⊦ e : τ     Γ, x : τ ⊦ f : σ
Γ ⊦ let x be e in f : σ

Soundness and completeness

The following properties describe the relation of typing to program execution.

Soundness: No incorrect programs are allowed.

Completeness: No correct programs are rejected.

Decidability of type checking: Type checking is decidable

We can define a type checking as a decision procedure for property “expression e has type τ but it evaluates to value v of type φ (φ ≠ τ)”. For this definition:

  • soundness means lack of false negatives (if expression is typed, the result of its evaluation has the same type)
  • completeness means lack of false positives (if expression e always evaluates to a value of type τ, e : τ is derivable during type checking)

Usually type systems for practical languages are sound and possibly decidable, hence incomplete (by Rice theorem of non-trivial property undecidability).

Soundness

Soundness: No incorrect programs are allowed.

Formal statement: if Γ ⊢ e : τ and during program execution expression e evaluates to a value v then v is of type τ.

Soundness is generally proved in two steps: preservation and progress.

e₁ ⟶ e₂ — during a single step of evaluation expression e₁ evaluates to expression e₂ (part of dynamic semantics, more formal definition on next lecture).

Preservation: Evaluation preserves typing.

Formally: Γ ⊢ e₁ : τ, e₁ ⟶ e₂ ⇒ Γ ⊢ e₂ : τ

Progress: If well-typed expression is not a value, it is possible to make an evaluation step.

Formally: Γ ⊢ e₁ : τ, e₁ is not a value ⇒ ∃ e₂ : e₁ ⟶ e₂.

Logical properties of typing

(usually are proved either by induction on rules or by induction on derivation)

Unicity: For every typing context Γ and expression e there exists at most one τ such that Γ ⊦ e : τ.

We usually want this property in a sane type system, it may be neccessary to use a different statement in case of subtyping (not a single type, but a single minimal/maximal type).

Inversion: (example) If Γ ⊦ plus(a, b) : num then Γ ⊦ a : num, Γ ⊦ b : num.

If typing rules are complex, such principles are difficult to state and prove. But these principles are essential for e.g. type inference.

Structural properties of typing

Weakening: If Γ ⊦ e : τ then Γ, x : σ ⊦ e : τ for x ∉ Γ. (we may add to context any number of typing judgements which do not overwrite the types of existing variables)

Contraction: (we may remove repeating judgements from context)

Γ, x : A, x : A ⊦ Σ
Γ, x : A ⊦ Σ

Exchange: (independent typing judgements may change order in context)

Γ₁, x : A, Γ₂, y : B, Γ₃ ⊦ Σ
Γ₁, y : B, Γ₂, x : A, Γ₃ ⊦ Σ

Substitution: (expressions with the same type may be substituted)

If Γ, x : τ ⊦ e’ : τ’ and Γ ⊦ e : τ , then Γ ⊦ [e/x]e’ : τ’

Decomposition: (we can factor out some typed value)

If Γ ⊦ [e/x]e’ : τ’ then for every τ such that Γ ⊦ e : τ, we have Γ, x : τ ⊦ e’ : τ’

Substructural type systems

Some type systems lack support for some of the mentioned structural properties.

Linear types

Based on the linear logic, ensures that each object is used exactly once. I.e. all objects have static lifetime controlled by type system. Doesn’t support weakening and contraction.

Affine types

Linear types with weakening (some variables may stay unused)

Affine types

In C++ affine types are implemented as std::unique_ptr:

std::unique_ptr<int> p1(new int(5));
std::unique_ptr<int> p2 = p1; //Compile-time error.
std::unique_ptr<int> p3 = std::move(p1); //Transfers the ownership. p3 now owns the memory and p1 is rendered invalid.

p3.reset(); //Frees the memory.
p1.reset(); //Does nothing.
See also: http://homepages.inf.ed.ac.uk/wadler/topics/linear-logic.html

Linear types

Clean programming language

AppendAB :: File -> (File, File)
AppendAB file = (fileA, fileB)
where
    fileA = fwritec 'a' file
    fileB = fwritec 'b' file -- compile-time error
WriteAB :: File -> File
WriteAB file = fileAB
where
    fileA = fwritec 'a' file
    fileAB = fwritec 'b' fileA
AppendAorB :: Bool *File -> *File
AppendAorB cond file
    | cond = fwritec 'a' file
    | otherwise = fwritec 'b' file
http://www.inf.ufsc.br/~joao.bosco.mota.alves/cleanBookI.pdf

Lifetimes and borrow checking (Rust)

Linear types provide simple, almost-syntactical value lifetime checking. More powerful lifetime tracking techniques are required in practice.

Patina: A Formalization of the Rust Programming Language ftp://ftp.cs.washington.edu/tr/2015/03/UW-CSE-15-03-02.pdf

RustBelt: Securing the Foundations of the Rust Programming Language https://dl.acm.org/doi/pdf/10.1145/3158154 https://plv.mpi-sws.org/rustbelt/popl18/appendix.pdf

See also:

RustViz: Interactively Visualizing Ownership and Borrowing https://arxiv.org/pdf/2011.09012.pdf

The Rust Programming Language. Chapter 4. Ownership and Borrowing. https://doc.rust-lang.org/book/ch04-02-references-and-borrowing.html

Type inference

In some languages it is possible to leave “holes” in place of type specifiers. Type checker tries to fill these holes in process of type inference (type reconstruction).

std::vector<std::map<int, bool>> m;
// ...
for (std::vector<std::map<int,bool>>::const_iterator it = v.begin();
  it != v.end(); ++it) { /* ... */ }

for (auto it=v.begin(); it != v.end(); ++it) {
  decltype(it) it2;
  /* ... */
}

Type inference

data List t = Nil | Cons (t, List t)

length l =
  case l of
    Nil -> 0
    Cons(x, xs) -> 1 + length(xs)


-- length :: List t -> Integer

Hindley-Milner Algorithm W

Most well-known algorithm for type inference: Hindley-Milner Algorithm W.

Algorithm is “bottom-up”: it assigns type variables starting from leaves of AST. Monotype: ordinary type, polytype has some type variables: ∀α.(Set α) → int

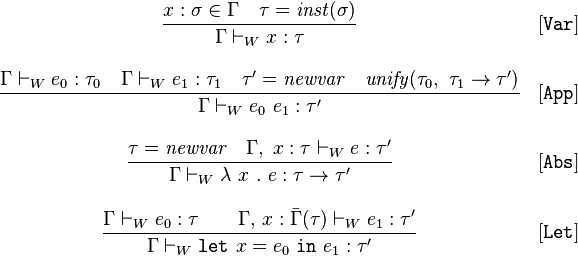
Sample implementations: https://github.com/tomprimozic/type-systems

http://dev.stephendiehl.com/fun/006_hindley_milner.html

http://reasonableapproximation.net/2019/05/05/hindley-milner.html

Algorithm M

“Algorithm M” is a top-down algorithm for type inference. It stops earlier than W if the input term is ill-typed and in some cases yields better type errors.

Oukseh Lee and Kwangkeun Yi. 1998. Proofs about a folklore let-polymorphic type inference algorithm. ACM Trans. Program. Lang. Syst. 20, 4 (July 1998), 707-723. http://dx.doi.org/10.1145/291891.291892

Subtyping

Type inference algorithms are undecidable in case of subtyping

Subsumption rule for subtyping:

Γ ⊦ t : T     T <: U
Γ ⊦ t : U

Row polymorphism

Row polymorphism is “duck typing” implementation for records (structures, named tuples).

Usual definition for structure type: [ t1 : T1, t2 : T2, … ]

{ a:1, b: "B"  } : [ a : Integer, b : String ]

Row polymorphism: [ t1 : T1, t2 : T2, … | τ] τ may be instantiated to extra fields.

 { a:1, b: "B" } : [ a : Integer | τ ]
 { a:1, b: "B" } : [ b: String | τ ]

function f(x) { return x.a + 1 }
f : [ a : Integer | τ ] → Integer

function g(x) { return x.b + "!" }
g : [ b : String | τ ] → String

Dynamic type checking

Dynamic type checking can be an implementation detail (for strongly-typed programming languages).

For example, GHC compiler for Haskell programming language has a flag -fdefer-type-errors:

{-# OPTIONS_GHC -fdefer-type-errors #-}
f :: Int -> Bool
f 1 = False
f 2 = not 'x' -- boolean "not" operator on string
/Users/rae/work/blog/011-dynamic/post.lhs:32:13: warning:
    • Couldn't match expected type ‘Bool’ with actual type ‘Char’
    • In the first argument of ‘not’, namely ‘'x'’
      In the expression: not 'x'
      In an equation for ‘ex1’: ex1 = not 'x'

If we call (f 2):

*** Exception: /Users/rae/work/blog/011-dynamic/post.lhs:32:13: error:
    • Couldn't match expected type ‘Bool’ with actual type ‘Char’
    • In the first argument of ‘not’, namely ‘'x'’
      In the expression: not 'x'
      In an equation for ‘ex1’: ex1 = not 'x'
(deferred type error)
https://typesandkinds.wordpress.com/2016/01/22/haskell-as-a-gradually-typed-dynamic-language/

Gradual typing

Gradual typing is a seamless combination of dynamic and static type checking.

Gradual typing introduces a special unknown type (usually denoted as ? or Any) with weakened form of type equivalence:

   
T ~ T
   
T ~ ?
   
? ~ T
T ~ U     V ~ W
T → V ~ U → W

Instances of an unknown type coercion to a known type are replaced with dynamic type checking. Implementations: TypeScript, Flow (for JavaScript); mypy (Python); Typed Clojure, Typed Racket

Implementation of typing

Static semantics environments → Typing environments

Typing judgements are represented as indexed inductive type constructor. To each typeable node of static semantics tree we must attach the corresponding typing judgement.

Example: http://mazzo.li/posts/Lambda.html

Recursive types

Example: simply-typed lambda calculus with iso-recursive types (B. Pierce. Types and Programming Languages, Chapter 20).

Additional terms: fold [T] t, unfold [T] t (T — type)

Additional value: fold [T] v (T — type)

Additional types: X (type-variable), μX.T (recursive type)

Additional evaluation rules:

   
unfold [S] (fold [T] v) ⟶ v
t ⟶ t’
fold [T] t ⟶ fold [T] t’
t ⟶ t’
unfold [T] t ⟶ unfold [T] t’

Additional typing rules:

U = μX.T     Γ ⊦ t : [X := U] T
Γ ⊦ fold [U] t : U
U = μX.T     Γ ⊦ t : U
Γ ⊦ unfold [U] t : U [X := U] T

Recursive types: example

Type of lists with argument — natural number.

Primitive types: ℕ, 𝟙 (type with single element, 1).

Additional type constructors: A + B (alternative), A * B (pairs)

ℕ-List : Type := μX.(1 + ℕ * X)

nil : ℕ-List := fold [ℕ-List] (inl 1)

cons : ℕ → ℕ-List → ℕ-List := λ (n : ℕ). λ (l : ℕ-List). fold [ℕ-List] (inr (n, l))

head : ℕ-List → 1 + ℕ := λ (l : ℕ-List). case (unfold [ℕ-List] l) of

    inl _ ⇒ inl 1

    inr (h, t) ⇒ inr h

System F: polymorphic lambda-calculus

Additional types: α (type variable), ∀α.T (polymorphic type)

Additional terms: Λα.t (type abstraction), t ∘ A (type application)

Additional typing rules:

Γ ⊦ t : B
Γ ⊦ Λα.t : ∀α.B
Γ ⊦ t : ∀α.B
Γ ⊦ t ∘ A : B[α := A]

Example: polymorphic identity function

Λα. λ(x : α). x : ∀α. α → α

Hindley-Milner type system is a simplified version of System F.

Data-type encoding in polymorphic lambda-calculus

In polymorphic lambda-calculus it is possible to define some data types in terms of elimination functions.

Boolean numbers

Bool = ∀ γ. (γ → γ → γ)

true = Λ γ. λ t. λ f. t

false = Λ γ. λ t. λ f. f

if (u : Bool) then (T : A) else (F : A) = (u ∘ A) T F

Sum-types (disjoint unions)

A + B = ∀ γ. ( (A → γ) → (B → γ) → γ)

inl a = Λ γ. λ f. λ g. (f a)

inr b = Λ γ. λ f. λ g. (g b)

Homework assignments

Task 6.1.** Implement Algorithm W for Hindley-Milner type inference in polymorphic lambda-calculus with data types.

Task 6.2.** Implement Algorithm M for type inference in polymorphic lambda-calculus with data types.

Task 6.3.*** Implement a type inference algorithm for a language with row polymorphism.

Task 6.4.*** Implement a type checking algorithm for a language with gradual typing.